A propos de la forme des miroirs…

Beaucoup de choses, plus ou moins vraies, se disent au sujet de la forme des miroirs. Nous allons essayer aujourd’hui d’aborder quelques notions d’optique afin de préciser ce dont il s’agit. Nous présenterons aussi les critères qui font d’un miroir, une bonne ou une mauvaise pièce optique. Nous ne considérerons dans cet article que les défauts de forme des optiques et non les défauts d’aspect (rayure, piqûre, filandre et micro-mamelonage)

Notion de front d’onde :

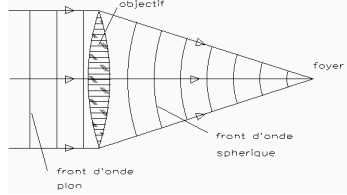
Imaginons une pierre lancée au milieu d’un étang. On peut constater, autour du point de chute, la présence de vagues concentriques s’agrandissant. Figeons l’image et dessinons un cercle autour du point de chute. Sur chaque point de ce cercle, l’eau est à la même hauteur (que ce soit entre deux vagues, au sommet d’une vague ou dans une pente). Chaque cercle que l’on peut dessiner autour de la source est un front d’onde. C’est un lieu où tous les points ont la même hauteur. De même que l’eau, la lumière est une onde. Cette onde est notamment caractérisée par sa longueur d’onde ; la distance séparant deux points haut de l’onde. On peut faire un rapprochement entre la pierre lancée dans l’eau et une étoile. L’étoile peut être considérée comme un objet ponctuel émettant de la lumière dans toutes les directions. Chaque sphère que l’on peut dessiner autour de l’étoile est aussi un front d’onde car sur cette sphère, l’onde lumineuse est au même niveau. En astronomie, on observe des étoiles très lointaines et on considère que les fronts d’onde venant des étoiles sont plans. La fonction d’un objectif parfait (que ce soit une lentille ou un miroir) est de déformer le front d’onde. A la sortie de l’objectif, le front d’onde doit être sphérique de façon à ce que le faisceau lumineux converge bien au foyer.

Conséquence d’un défaut de forme sur le front d’onde

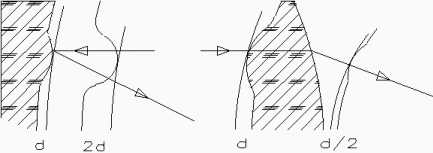
Un défaut sur une surface optique de l’objectif entraînera un défaut sur le front d’onde émergeant de l’optique. Mais le front d’onde ne sera pas altéré de la même façon si l’objectif est une lentille ou un miroir. Supposons que le défaut soit une bosse. Sur un miroir, un point du front d’onde atteindra la bosse en premier et se réfléchira dessus alors que le reste du front d’onde n’a pas encore atteint le reste du miroir. Lorsque la totalité du front d’onde se sera réfléchi, on pourra observer sur ce dernier un défaut deux fois plus grand que le défaut de l’optique. Dans le verre d’une lentille, le front d’onde se déplace plus lentement. Le rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans le verre défini l’indice du verre. Cet indice se trouve autour de 1,5 pour la majorité des verres. Donc, lorsque le front d’onde atteint le verre, il ralentit avec une vitesse dépendant de l’indice. Le reste du front d’onde se déplaçant alors plus vite, devance un peu la partie ayant traversé la bosse. Donc, l’influence du défaut est moindre. En fait le défaut du front d’onde est égal à la moitié du défaut de la surface optique pour un indice de 1,5. Lorsque l’on caractérise un défaut optique, il faut faire attention, car on peut parler du défaut de la surface (défaut mécanique ou sur le verre) ou l’on peut parler du défaut du front d’onde émergeant de l’optique. En général, les opticiens utilisent le défaut du front d’onde (du moins en France, car aux USA, le défaut mécanique est plus utilisé), mais certains revendeurs de miroirs peu scrupuleux utilisent de défaut sur le verre sans le préciser. Il est donc indispensable de se faire préciser la règle exprimant le défaut.

Rayon de courbure, focale et parabole.

Si l’on place un objet A en un lieu proche du centre de courbure d’un miroir sphérique, chaque rayon lumineux peut être considéré comme un rayon de la sphère. Comme tel, il est normal (perpendiculaire) à la surface et se réfléchit presque sur lui-même formant l’image B de l’objet A. Si par contre l’objet est à l’infini (cas de l’astronomie), les faisceaux lumineux ne sont plus normaux au miroir. Ils sont réfléchis en formant une image au Foyer située a mi-chemin du centre de courbure et le centre du miroir (sommet). Donc la distance focale d’un miroir est égale à la moitié du rayon de courbure. Si l’on raisonne en terme de front d’onde, l’onde sphérique issue de l’objet A se réfléchit sur le miroir (en restant sphérique) pour converger sur l’image B. Comme l’onde réfléchie est sphérique l’image B est de bonne qualité. Par contre, on montre que le front d’onde plan issu d’un objet à l’infini ne se réfléchit pas sur une sphère en donnant une onde sphérique. L’image de l’objet au foyer n’est pas de bonne qualité. On constate que les rayons lumineux se réfléchissant près du centre du miroir convergent bien au foyer, mais on observe que ceux se réfléchissant près du bord du miroir se coupent en un point plus près du miroir. Pour que les rayons lumineux convergent tous au foyer, il faut ouvrir un peu les bords du miroir. On montre que la forme idéale est une parabole. Seule la parabole permet d’obtenir une onde réfléchie parfaitement sphérique pour une onde plane situé sur l’axe. On dit que le miroir sphérique souffre d’une aberration de sphéricité, tandis que le miroir parabolique n’en a pas (tout au moins pour le cas qui nous intéresse, c’est à dire l’objet à l’infini).

La distance entre le point où se croisent les rayons venant au centre du miroir et le point où se croisent les rayons venant du bord du miroir est appelée aberration longitudinale. Si l’on prend un plan, perpendiculaire à l’axe optique, situé autour du point focal, le diamètre de la tache fait par les rayons lumineux est appelé aberration transversale. L’endroit où l’aberration transversale est minimale est appelé cercle de moindre aberration. Lorsque l’on mesure un miroir à l’aide d’un appareil de Foucault, par exemple, le miroir n’est pas utilisé dans les conditions ci-dessus : La source lumineuse et l’image se trouvent au centre de courbure. Dans ce cas, c’est le miroir parabolique qui possède une aberration de sphéricité. C’est précisément en mesurant l’aberration longitudinale (conséquence de l’aberration de sphéricité) à l’appareil de Foucault que l’on mesure la forme des miroirs.

Coefficient de déformation et coniques

Pour le télescope le plus simple, le Newton, le miroir primaire se doit d’être parabolique. Mais certaines formules de télescope nécessitent d’autres formes de miroirs. Dans la quasi-totalité des cas, les miroirs ont une forme de la famille des coniques. Cette famille de courbe peut- être obtenue par différentes coupes par des plans dans un cône. La forme peut-être une sphère, une ellipse, une parabole ou une hyperbole. Ces courbes sont caractérisées par un coefficient de déformation (par rapport à la sphère) que l’on note b.

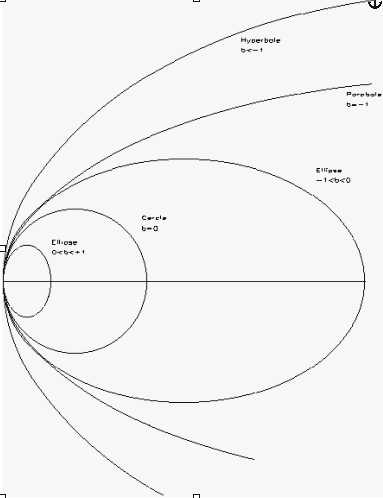
B est égal à 0 pour une sphére. Lorsqu'il est supérieur à 0 il s'agit d'une ellipse (le grand coté). Lorsque b est compris entre 0 et -1, il s'agit d'une ellipse (le bout de l'ellipse). Pour b=-1, c'est une parabole, pour b plus petit que -1, c'est une hyperbole

On voit sur le graphique ci joint la relation existant entre les différentes formes. On peut noter que toutes les courbes sont tangentes en leurs sommets. Elles ont toutes le même rayon de courbure au sommet. Lorsque le miroir dont on parle n’est pas sphérique (asphérique), on peut le comparer à au moins trois sphères différentes.

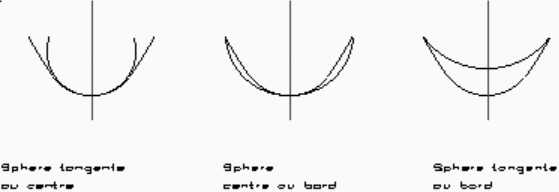
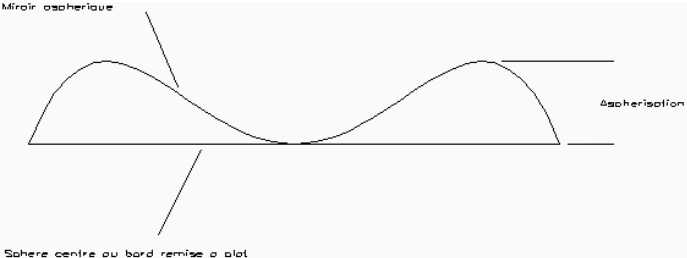
La sphère tangente au centre du miroir, la sphère passant par le centre et le bord du miroir, et la sphère tangente au bord du miroir. Le rayon de courbure d’un miroir asphérique est égal au rayon de la sphère tangente au centre. Néanmoins, pour les contrôles, on a plutôt tendance à utiliser la sphère centre au bord, dont le rayon diffère peu du rayon de courbure. Quelle est l’écart de forme d’un miroir asphérique par rapport à la sphère centre au bord ? On constate que la forme présente deux bosses qui sont situées à une zone qui est égale à 0,7 rayons du centre du miroir. La hauteur de cette bosse est appelée asphérisation, c’est à cet endroit que l’on trouve le plus grand écart entre la forme du miroir et la sphère centre au bord. Si la forme du miroir est issu d’une conique, on trouve toujours la même forme, seule la valeur change (et parfois le sens, comme par exemple, dans le cas d’un miroir convexe ou d’un coefficient d’asphérisation compris entre 1 et 0). On montre que la valeur de l’asphérisation est égale à :

Avec : b : Coefficient d’asphérisation h : Demi-diamètre du miroir R : Rayon de courbure du miroir Le demi-diamètre du miroir et le rayon de courbure doivent être exprimés dans la même unité que le résultat. Cette valeur donne l’asphérisation mécanique ou sur le verre. Pour la valeur sur l’onde, il faut donc multiplier par 2. L’asphérisation d’un miroir est donc dotant plus importante que le miroir est grand, et que le rapport F/D est court. Le polissage d’un miroir est plus difficile si l’asphérisation est importante. C’est donc pour cela que l’on conseil aux constructeurs amateurs de commencer par des miroirs pas trop grands ni trop ouverts.

Définir le défaut d’un miroir

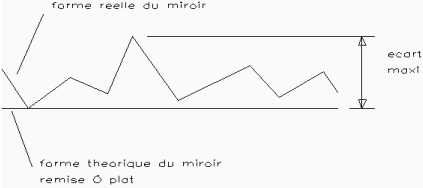
Comment définir la précision d’un miroir ? La première idée est de comparer la forme du miroir par rapport à la forme théorique (remise à plat) et de noter l’écart maximum. Bien souvent, on ne donne pas directement la taille du défaut, mais sa taille par rapport à la longueur d’onde utilisée par l’instrument. Cela est une bonne démarche, car en fonction du domaine de longueur d’onde observé, on n’a pas besoin de la même précision. On note la longueur d’onde l (lambda). Pour un télescope, on utilise la longueur d’onde moyenne du spectre visible (550 nanomètres). On dit par exemple que le défaut maximum est de 0,2 l ou encore l/5. Avec cette manière, on parle de défaut PtV (Pic to Valley). Il faut faire attention aux optiques issues de l’industrie, car le plus souvent le lambda fait alors 632.8 nm. C’est la longueur d’onde des bancs interférométriques permettant de mesurer les optiques. Ainsi, une optique à l/12 pour le centre du spectre visible sera mesurée à l/14 pour une longueur d’onde de 632,8 nm. Mais ce n’est pas forcément une bonne manière de donner la précision d’un miroir. Les trois miroirs suivants montrent un même PtV, pourtant, ils ne sont pas de la même qualité.

Ils sont classés par ordre de qualité du plus mauvais au meilleur. On voit qu’un défaut local peut influencer grandement le PtV, bien que le miroir reste un bon miroir. Il est donc nécessaire de définir le défaut de forme du miroir par une autre quantité. On définit un défaut moyen du miroir comme un écart quadratique moyen ou RMS (pour Root Mean Square). Bien que les trois miroirs de l’exemple possèdent le même PtV, le premier a un RMS plutôt élevé, tandis que le troisième aura un RMS plus faible. Le défaut RMS est donc plus représentatif du défaut des miroirs. Une autre valeur permettant de définir la qualité d’un miroir est la pente. Ce chiffre est caractéristique du fait que certaines parties du miroir sont plus ou moins inclinées par rapport à l’horizontal. De la même façon que sur la forme du miroir, on parle de PtV des pentes (pente max.) et de RMS des pentes (moyenne des pentes). Le miroir n°3 aura un PtV des pentes très élevé, tandis que sont RMS sera plutôt faible. Le miroir n°1 aura un PtV de pentes inférieur, mais par contre son RMS sera nettement plus élevé. En général, lorsque l’on ne donne qu’un chiffre il s’agit du PtV. Mais on constate que cela est bien insuffisant. Il faudrait idéalement avoir le PtV, le RMS et les pentes pour juger de la qualité d’un miroir. Si la précision est donnée en l, il faut bien se faire préciser la longueur d’onde utilisée. Faites attention, car certains revendeurs vendent du RMS pour du PtV. Il faut savoir que, pour la plupart des miroirs, le RMS est 3 à 6 fois plus petit que le PtV (4 en moyenne).

Quelle doit être la précision d’un miroir ?

L’image d’une étoile fournie par un télescope n’est pas un point. Si l’on regarde avec un très fort grossissement, on constate que l’image est faite d’un cercle (tache de diffraction, ou disque d’Airy) entouré d’anneaux concentriques de plus en plus faibles (anneaux de diffraction). La taille angulaire de la tache de diffraction définie le pouvoir de résolution du télescope. Cette taille ne dépend que du diamètre de l’optique. Dans le cas d’une optique parfaite, on trouve environ 84% de la lumière dans la tache de diffraction et donc 16% dans les anneaux. Si l’optique n’est pas parfaite, la tache de diffraction devient moins lumineuse au profit des anneaux limitant ainsi le pouvoir de résolution du télescope. Si l’on consulte la littérature sur le sujet, on constate que les différents auteurs ne sont pas toujours d’accord. Mais l’un des critères le plus utilisé est celui qui a été fixé par Lord Rayleigh. Cet homme dit qu’il fallait qu’une optique fournisse un front d’onde mieux que l/4 PtV, pour que l’image soit proche de la perfection (à condition d’avoir des pentes faibles, car Rayleigh fit son calcul pour une aberration de sphéricité). Pour information, un miroir qui satisfait au critère de Rayleigh fourni une image de diffraction avec 68% de l’énergie dans la tache de diffraction et 32% dans les anneaux. Parfois, on utilise le Strehl ratio pour caractériser une optique. Il s’agit du rapport entre l’intensité lumineuse max (au centre de la tache de diffraction) de l’optique considérée et d’une optique parfaite. Le Strehl ratio est donc égal à 1 pour une optique parfaite, il est égal à 0,8 pour un miroir satisfaisant le critère de Raleigh. Les télescopes de type 115/900 sont équipés de miroirs primaires sphériques. Si l’on fait le calcul de l’asphérisation d’un tel miroir, on constate de cette dernière est égale à 0,117 microns soit approximativement l/5. Donc, le miroir sphérique d’un 115 est une parabole avec une défaut de l/5. Cela explique que dans certain cas, des miroirs sphériques peuvent donner d’excellentes images. Contrairement à ce que l’on pourrait croire, un miroir qui satisfait au critère de Rayleigh est un très bon miroir. Il faut savoir que la majorité des télescopes amateur du commerce sont autour de l/2 PtV et l/10 RMS. Cela signifie que très peu de télescopes du commerce sont capables de satisfaire au critère de Rayleigh. D’autres critères existent. Le critère de Maréchal est défini par l/16 RMS (donc l/4 PtV). Le critère de Françon est de l/16 PtV. C’est la limite au-delà de laquelle on ne pourra pas faire la différence avec une optique parfaite. Dans l’optique professionnelle aussi, une optique à l/4 PtV est considérée comme une bonne optique. A l/10 PtV, la pièce est considérée comme un calibre de référence.

Méthode de mesure de la précision d’un miroir.

Le couteau de Foucault est la méthode la plus employée pour mesurer les miroirs chez les amateurs, car c’est la plus simple. Lorsque l’on mesure un miroir au Foucault, on mesure un PtV du miroir. Mais comment ce fait-il que certains amateurs annoncent fièrement avoir fini leurs miroirs à l/20, l/25 ou même plus encore ? En fait, ce résultat surprenant est la conséquence de la méthode de mesure. On place devant le miroir un écran avec des fenêtres alignées. On analyse donc le miroir que sur un diamètre. On ne peut voir, au Foucault, qu’un défaut ayant une symétrie de révolution. Tous les défauts de non-révolution sont tout simplement ignorés (astigmatisme, et défauts locaux principalement). Le problème vient aussi de l’échantillonnage. Dans le cas du Foucault, on place un écran ayant 4 à 10 fenêtres maximum. Avec un banc interféromètrique, le diamètre de l’optique peut être analysé sur 100 voir 200 pixels de la caméra du banc (ce qui fait pour un miroir rond 6000 à 24000 points de mesures pour les bancs interféromètriques les plus performants!). Pour connaître la forme exacte d’un miroir, il est préférable de l’analyser à l’aide d’un banc interféromètrique, mais cela est malheureusement hors de portée des amateurs. Pour la petite histoire, l’année dernière j’ai réalisé un miroir de 200mm. En court de travail, j’ai décidé de comparer les mesures que je faisais au Foucault avec celle d’un banc interféromètrique. Ayant mesuré mon miroir, au Foucault, à l/6 PtV, j’eus une grande surprise en le mesurant au banc interféromètrique. Mon l/6 PtV s’était transformé en l/6 RMS et l/1,5 PtV… On peut tout de même se dire qu’un miroir à l/15 ou l/20 PtV au Foucault est un bon miroir, a condition qu'il ne possède pas d'astigmatisme, même si ce chiffre n’est pas égal à la qualité réelle du miroir. Si on veut être sur que son miroir soit bon, il est indispensable d’aller plus loin que le simple test de Foucault. Il est indispensable par exemple de contrôler l’astigmatisme en remplaçant le couteau par un oculaire (avec une source ponctuelle). Il vaut mieux aussi pratiquer le test au fil (variante du test de Foucault), ou encore le test de la caustique… Il faut donc se méfier pour juger de la qualité d’une optique. Le l ne fait pas tout, de plus, lorsque l’on annonce un l, il faut se faire préciser les choses. Quel est la longueur d’onde du l, s’agit-il de la précision de l’onde (optique) ou du verre (mécanique) ? S’agit-il d’une précision PtV ou RMS ? Quelles sont les pentes du miroir et avec quel moyen de contrôle le miroir a-t-il été mesuré, et surcombien de points de mesure ?

Écrit par Patrick Sogorb
http://www.astrosurf.com/sogorb