où
est le nombre de
combinaisons de n objets pris p à p. La série du binôme
est
convergente, de somme (1+x)m si
<
1, divergente si 
1.
Ses découvertes fondamentales en physique et en mathématiques
font de lui l'un des scientifique les plus connus de tous les
temps. Son nom reste en particulier attaché à la loi de la
gravitation (loi de l'attraction universelle), ainsi qu'à
la mécanique dite newtonienne qui prévalut jusqu'à l'avènement
de la relativité.
En optique, il s'intéressa à la dispersion de la lumière, après
avoir étudié la réfraction à travers les prismes (1666) et
montré ainsi que la lumière blanche est composée de rayons de
plusieurs couleurs. Il en déduisit une théorie des couleurs,
fondée également sur ses expériences dans le domaine des
interférences (anneaux de Newton). Il fut le tenant d'une
conception corpusculaire de la lumière qui l'opposa à Huygens.
Il construisit le premier télescope à miroir parabolique, éliminant
ainsi l'aberration chromatique due aux lentilles des lunettes en
(1668).
Dans ses Philosophiae naturalis principia mathematica (1687),
il exposa les trois lois fondamentales de la dynamique :
- le principe d'inertie, qui stipule que, dans un référentiel
galiléen, un corps qui n'est soumis à aucune force conserve sa
vitesse.
-le principe fondamental de la dynamique, qui exprime la
proportionnalité de la force F et de l'accélération
a d'un corps de masse S F
= dp / dt)
- le principe de l'action et de la réaction : à toute
force exercée par un corps A sur un corps B correspond la force
opposée de B sur A.
Il y exposa également la loi de l'attraction universelle
(1665), qui explique en particulier la pesanteur et l'attraction
des planètes par le Soleil. C'est d'ailleurs en appliquant les
principes fondamentaux de la dynamique pour expliquer les lois de
Kepler, que Newton fut amené à cette loi. L'ensemble de ces
principes constitue le fondement de la mécanique newtoniennne.
Il fit par ailleurs une des première théories de la propagation
du son.
En mathématiques, il développa le calcul infinitésimal en même
temps que Leibniz, mais indépendamment de lui. Il définit
notamment la dérivée ou "fluxion" (c'est-à-dire la
pente) comme un "quotient ultime de deux accroissements évanescents"
(car ils tendent vers zéro).
Il montra que la recherche de l'aire comprise sous une courbe (ou
quadrature) et la recherche des tangentes correspondent à deux
opérations mathématiques inverses (intégration et dérivation).
On lui doit la méthode de Newton-Raphson de résolution
numérique des équations (améliorée par Raphson), la formule
du binôme de Newton, le calcul de séries et le développement
en séries entières de fonctions, notamment de la fonction
arcsinus.
Il fut le premier à développer en série entière les solutions
d'une équation différentielle, étendant (sans démonstration,
certes) la validité de l'intégration d'une somme finie terme à
terme à une série infinie. On lui doit une classification des
courbes planes du troisième degré et l'introduction des
coordonnées polaires. Il aborda la mécanique analytique,
application du calcul différentiel (dérivées, tangentes,...)
à l'étude des mobiles et de leurs trajectoires.
Loi de l'attraction universelle
Loi selon laquelle la force d'attraction F entre deux points
pesants M1 et M2 est proportionnelle au
produit de leurs masses m1et m2 et
inversement proportionnelle au carré de la distance D qui les sépare
F = G m1m2 / D2, où G est la
constante de la gravitation universelle valant 6.673 10-11
(unités S.I.).
Loi du transfert thermique selon laquelle le flux de chaleur entre deux corps est proportionnel à leur différence de température. Ainsi, la densité de flux de chaleur à l'interface des deux corps (présentant une différence de température DT) est de la forme F = h DT, h étant le coefficient de transfert thermique. Cf. loi de Fourier.
Loi de Newton (rhéologie)
Loi (de rhéologie) exprimant les forces de viscosité T (par
unité de surface) dans un écoulement : T = m
¶V/¶y où m
est la viscosité dynamique, y
une direction perpendiculaire à celle de la vitesse V.
Liquide newtonien, non-newtonien.
Anneaux de Newton
Figure d'interférence consistant en des anneaux concentriques apparaissant au niveau du coin d'air délimité par une surface plane et une lentille. cf. Young.
Binôme de Newton
Formule (valable dans tout anneau) :
où est le nombre de
combinaisons de n objets pris p à p.
La série du binôme est
convergente, de somme (1+x)m si<
1, divergente si 1.
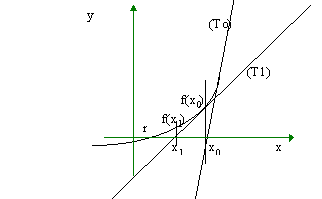
Méthode de Newton-Raphson (ou des tangentes)
Méthode de recherche des racines d'une équation
f(x)=0. Cette méthode est itérative et consiste à chaque pas
à utiliser l'intersection entre l'axe des x et la tangente à la
courbe (au point obtenu précédemment). Elle s'écrit dont xn+1
= xn -f(xn)/f'(xn). La vitesse
de convergence est quadratique, lorsque l'on est dans un cas de
convergence ce qui dépend de la position du point initial en
fonction de la forme de la courbe. Cf. dichotomie. En dimension
supérieure à un la méthode s'applique à la résolution de
systèmes d'équations linéaires représentés par des équations
F(X) = 0 où X = (x1, ... ,xn) est un vecteur. On choisit un
vecteur initial Xo et applique la relation de récurrence J (Xm)
(Xm - Xm+1) = - F(Xm), où J(Xm)
est la matrice jacobienne de F en Xm (de terme général
). La suite (Xm)
converge vers la solution du système, si elle converge.
Newton (Unité)
Unité S.I. de force (N) correspondant à la force qui communique à une masse de 1 kg une accélération de 1 m.s-2. (1N = 1m.kg.s-2).