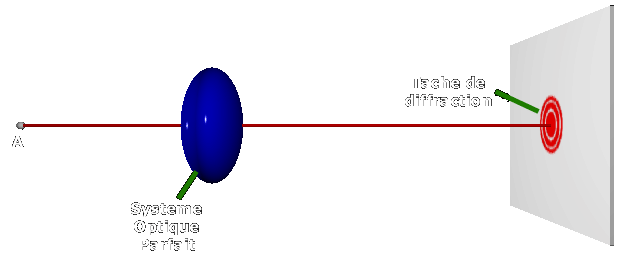
La diffraction

Les instruments astronomiques constituent des systèmes optiques ayant pour but d'associer un espace dit "objet" à un espace image. A travers l'oculaire, nous visualisons l'espace "image". Évidemment, il doit être le plus fidèle possible de l'image d'origine. En optique, on appelle cela travailler dans les conditions de Gauss, en assurant un stigmatisme rigoureux entre le point objet A (une étoile par exemple) et son point image A' (la même étoile vue à l'oculaire) : il faut que la distance AA' soit constante.

Cette condition est rarement réalisée rigoureusement. Les rayons issus de A ne font que passer au voisinage de A. On a alors affaire aux aberrations. Ce sont les lunettes bon marché qui subissent, en général, ce problème. L'objectif d'une lunette est très complexe et doit être très précis dans sa conception. On peut ainsi réduire jusqu'à annuler les aberrations (en y mettant le prix!). Les télescopes n'ont pas ce problème car les miroirs réfléchissent la lumière, qui elle, n'a pas à traverser une couche de verre. Mais, même dans la cas d'un stigmatisme rigoureux, pour un miroir parabolique par exemple, on n'obtient pas une image ponctuelle. Les montures des lentilles et des miroirs, en général circulaires, limitent les faisceaux de lumière et introduisent une certaine diffraction. L'image d'une étoile n'est donc pas ponctuelle, mais est en fait une tache de diffraction correspondant à une tache d'Airy entourée d'anneaux concentriques. Cependant, cette figure de diffraction n'est réellement visible qu'aux grands grossissements (plus de 1,5 fois le diamètre de l'instrument).
Le phénomène de diffraction apparaît donc comme la limite ultime de la notion d'image ponctuelle.

C'est ce qui explique l'existence d'un pouvoir de résolution. C'est la capacité d'un instrument astronomique à séparer 2 images ponctuelles à l'infini (une étoile double par exemple). En dessous d'une certaine distance radiale entre 2 composantes d'une étoile double, l'instrument n'est plus en mesure de séparer les 2 étoiles, et ceci quelque soit le grossissement utilisé.

Ceci dit, l'observation de la figure de diffraction va nous renseigner considérablement sur la qualité de l'instrument utilisé. Si on observe un système régulier d'anneaux, c'est que la réalisation optique est de très bonne qualité. Mais le test connu de tous les amateurs est de connaître la limite de résolution du télescope en visant une étoile double dont l'écart des composantes est connu, et en regardant si elles sont résolues. Si tel est le cas, le pouvoir de résolution est inférieur ou égal à la valeur de l'écart angulaire.

Critère de perfection des instruments d'optique : le critère de Rayleigh

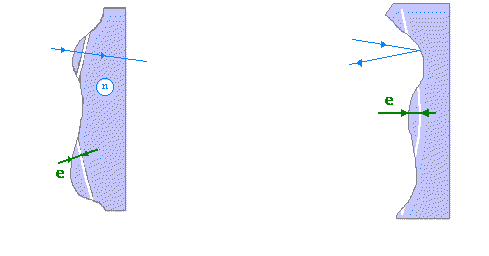
La diffraction est due aux inhomogénéités des surfaces optiques en jeu. La différence accidentelle entre la surface parfaite et le surface réelle de l'objectif ou du miroir induit ce qu'on appelle une différence de marche sur les chemins optiques. Pour un objectif d'indice de réfraction n :

delta = (n-1)*e
Pour un télescope delta =2*e
où e est la distance entre la surface parfaite et la surface réelle

Le critère de Rayleigh dit qu'il faut que  la longueur d'onde de la lumière de l'étoile ( pour la lumière dans le domaine du visible: 410nm (violet) < lambda < 750nm (rouge)
On calcule ainsi qu'un bon miroir doit satisfaire e < lambda/8. Un miroir dont les plus grands inégalités mesurent cette valeur est dit être " à lambda sur 8".